Bridging the gap between atomically thin semiconductors and metal leads – Nature.com
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
Advertisement
Nature Communications volume 13, Article number: 1777 (2022)
7353
18
3
Metrics details
Electrically interfacing atomically thin transition metal dichalcogenide semiconductors (TMDSCs) with metal leads is challenging because of undesired interface barriers, which have drastically constrained the electrical performance of TMDSC devices for exploring their unconventional physical properties and realizing potential electronic applications. Here we demonstrate a strategy to achieve nearly barrier-free electrical contacts with few-layer TMDSCs by engineering interfacial bonding distortion. The carrier-injection efficiency of such electrical junction is substantially increased with robust ohmic behaviors from room to cryogenic temperatures. The performance enhancements of TMDSC field-effect transistors are well reflected by the low contact resistance (down to 90 Ωµm in MoS2, towards the quantum limit), the high field-effect mobility (up to 358,000 cm2V−1s−1 in WSe2), and the prominent transport characteristics at cryogenic temperatures. This method also offers possibilities of the local manipulation of atomic structures and electronic properties for TMDSC device design.
With a geometry similar to that of graphene, atomically thin transition metal dichalcogenide semiconductors (TMDSCs) possess many valuable properties that further broaden the two-dimensional (2D) materials playground1,2,3. However, in contrast to graphene, the electrical performance of atomically thin TMDSC field-effect transistors (FETs), such as the carrier mobility at cryogenic temperatures, is generally insufficient to explore many quantum transport properties or practical applications4,5,6. Electrically interfacing atomically thin TMDSCs with metal leads is inherently problematic because of undesired metal-semiconductor interface barriers. These include the tunnel and Schottky barriers as shown in Figs. 1a, b, respectively. Fermi-level pinning effects and Schottky barriers naturally arise when defect-induced gap states occur at the interface7,8. These interfacial barriers dramatically suppress the carrier-injection efficiency by capping the available carrier mobility and presenting large contact resistance in TMDSC FETs.
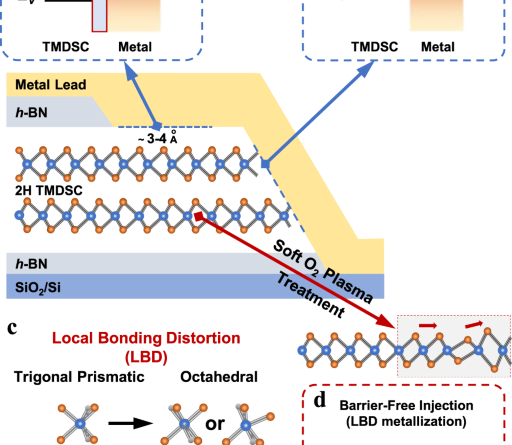
a Interfacial band alignment of the van der Waals (vdW) contact. b Interfacial band alignment of the Schottky-limited contact. c Atomic configurations of [TM-C6] polyhedra and corresponding energy splitting diagrams of Mo/W d-orbitals before and after the local bonding distortion (LBD). d Interfacial band alignment of the contact utilizing LBD mechanism. EC and EV represent the energy of conduction and valence band edges in TMDSCs, respectively. EF indicates the Fermi-level energy in metal leads while ΦB denotes the Schottky barrier height. Blue arrows suggest the routes for carrier injection, where e− indicates the electron branch.
Great efforts have been made over the past decade to minimize the electrical contact barriers in TMDSC FETs, which can be grouped into two major categories: (I) direct metallization of the contact region through doping treatments9,10,11 or microscale phase transformation12,13,14, and (II) van der Waals (vdW) contacts by inserting tunnel-barrier layers into the metal-semiconductor junction15,16, or by using graphene/soft-landed metals as vdW-interfaced electrodes17,18,19,20,21,22,23. It is notable that through extra gating on the contact regions, graphene leads can eliminate Schottky barriers in few-layer MoS2 FETs17,18. In this case, however, the inherent nature of vdW contacts still limits the charge carrier injection, because the large vdW gap (3–4 Å) between the metal lead and TMDSC surface acts as an additional tunnel barrier against the carrier flow.
An efficient carrier injection to the conduction or valence bands of TMDSCs requires effective orbital overlap or hybridization between the transition metal and the electrode atoms. For example, the conduction band minimum of monolayer TMDSCs arises mainly from the d-orbitals of transition-metal atoms24, which are sandwiched by two layers of chalcogen atoms. Any carrier injection through the chalcogen surface of TMDSCs (i.e., across the vdW gap) is less efficient because the orbitals of chalcogen atoms contribute little to the energy band edges. Alternatively, an edge-contact strategy can offer the advantage of orbital hybridization to transition-metal atoms25. However, Fermi-level pinning effects caused by the dangling bonds of TMDSCs edges inevitably result in severe Schottky barriers, degrading the FET performance at low temperatures (Supplementary Fig. 1). Since rich quantum transport behaviors of fundamental importance, such as topological states and electron correlation effects, are completely perturbed by the thermal stimulation and the strong phonon scattering of atomically thin TMDSC channels at room temperature, probing fascinating condensed matter physics in TMDSCs requires the significant advance in their low-temperature contact performance.
To address these issues, we develop a local bonding distortion (LBD) strategy for realizing highly efficient electrical junctions with atomically thin TMDSCs down to the monolayer limit. Both atomic-resolution cross-section electron microscopy and Raman spectroscopy evidence the LBD as a nanoscale trigonal-prismatic-to-octahedral coordination change of metal-chalcogen polyhedra in the metal-TMDSC interface. The LBD region acts as a semi-metallic bridge between the metal lead and the pristine TMDSC channel, exhibiting robust ohmic behaviors from room to cryogenic temperatures. The LBD contacts significantly elevate the carrier-injection efficiency of TMDSC FETs, demonstrating the low contact resistance down to 90 Ωµm in 3L-MoS2 and the high field-effect mobility up to 358,000 cm2V−1s−1 in 5L-WSe2 with prominent transport characteristics at 0.3 K. This work not only paves the way to exploring the unconventional quantum transport properties in TMDSCs, but also provides a scheme in the local manipulation of atomic structures and electronic properties of TMDSCs. We note that there are pioneering contact improvement works by argon-plasma-induced T phase14, but the energetic argon bombardment actually creates vacancies to stabilize the phase transition, which is different from our structurally seamless soft oxygen plasma method. And our LBD is not the conventional 1 T phase transition, but an intermediate structure towards tetragonal phases without vacancies or dangling bonds. Our work establishes an innovative approach to enhancing the orbital hybridization and carrier-injection efficiency in metal-TMDSC contacts in a highly controllable way, which have not been dealt with in previous reports.
First of all, we would like to introduce the basic mechanism of our LBD strategy. As shown in Fig. 1c, due to the trigonal-prismatic coordination of [TM-C6] polyhedra in the H structure (in which TM stands for the transition metals, and C stands for the chalcogen atoms), the TM4+ d-orbitals exhibit a close-shell electronic configuration (two d-electrons with opposite spins in one orbital) without itinerant electrons, resulting in semiconducting properties. In contrast, the octahedral coordination after distortion owns a rearranged energy splitting for the TM4+ d-orbitals. The partial filling of two d-electrons with parallel spin into the three-fold degenerate orbitals provides both unoccupied states and itinerant electrons, resulting in the metallicity of the material26. The local distortion of [TM-C6] polyhedra from trigonal-prismatic coordination to octahedral one modulates the electronic property into semi-metallicity, offering dispersed density of states (DOS) along the TMDSC energy band gap, and thus forms nearly barrier-free electrical interfaces as illustrated in the interfacial band diagram of Fig. 1d. Such lattice distortion is different from destructive defects and has been applied to engineer bulk materials’ properties27,28, while it has not been reported in TMDSCs yet. It is also different from the common H-to-T phase transition in TMDSCs by its nanoscale sizes and tunable work functions (Supplementary Fig. 11).
Technically, we chose pure oxygen (a chalcogen element) plasma to trigger the LBD in the contact interfaces of several representative 2D semiconductors, including MoS2 and WSe2. Schematics in Fig. 2 show the workflow of our referenced reactive ion etching (RIE) processes to fabricate LBD structures in both edge- and top-contact geometries. A thin poly(methyl methacrylate) (PMMA) mask is defined by e-beam lithography for the simultaneous RIE of the contact windows and the reference area. By monitoring the optical contrast of the reference area, either a top-BN/TMDSC/substrate region in the edge-contact geometry or a top-BN/substrate region in the top-contact geometry, the etching depth in contact windows is controlled precisely (the optical contrast of 300-nm-SiO2/Si substrate will be totally different without 2D materials coverage). Followed by the tuned soft oxygen plasma treatment, LBD appears on the exposed TMDSC edges or surfaces for different contact geometries. We want to emphasize that the oxygen plasma treatment is configured in a soft-landing manner to avoid generating defects in TMDSCs by paralleling the capacitively coupled electrostatic field along the sample surface, reducing the plate bias and lowering the input power. More details of the FET fabrication can be found in the Method section and step-by-step images in Supplementary Fig. 2. The LBD is reproducible once suitable conditions are set up. With reasonable proposals, we are pleased to provide devices utilizing LBD contacts for collaborative research.
Schematics showing the workflow of fabricating LBD contacts to BN-encapsulated TMDSCs in both edge- and top-contact geometries. After the soft oxygen plasma treatment, LBD appears on the exposed TMDSC edges or surface for the edge- and top-contact geometries, respectively.
Our LBD contact strategy works perfectly in the edge-contact geometry for exploiting its strong orbital overlap and hybridization advantages as demonstrated by 3L-MoS2 FETs. In the top and cross-section views of Figs. 3a, b, after electrical measurements, a cross-section membrane from one of the main electrical contacts was lifted out for the electron microscopy observation. In the low-magnification annual dark field (ADF) image of the contact region (Fig. 3c), the elegant edge-cutting of the BN-MoS2-BN stack by the referenced RIE process can be observed. The electrical interface between the 3L-MoS2 edge and the deposited metal was observed at atomic resolution along the zig-zag direction, as shown in Fig. 3d. The atomic-resolution ADF image shows three main structural features of the plasma-induced LBD in the edge-contact region: (1) the LBD localizes within the ~1 nm wide edge of 3L-MoS2; (2) both Mo and S atomic positions deviate from the ideal 2H phase on the left and form octahedral configurations; (3) terminated Mo atoms at the MoS2 edge connect directly to the lead surface atoms with a closest distance of ~1.8 Å, which is much smaller than the normal vdW gap size (~3–4 Å) and similar to that of a typical chemical bond. This atomic-scale observation supports the strong orbital overlap and hybridization between transition-metal and electrode atoms in an edge-contact geometry.
a Top-view optical image of a typical 3L-MoS2 FET. The dash-dot line indicates the cutting position in the source, from which a cross-section membrane as illustrated in the schematic (b) was extracted using the focused ion beam (FIB) method. c The low-magnification ADF image of the contact region. The area in the red-dash rectangle is zoomed in as (d). d Atomic-resolution ADF image of the MoS2-LBD-metal junction observed along the MoS2 zig-zag direction. The first layer of MoS2 is analyzed in (e) with the corresponding atomic model shown below. The overlaid blue, red and green dashed lines highlight the lattices of hexagonal MoS2, octahedral MoS2 and metal lead, respectively. f The Mo–Mo bond-length comparison (E equal, S short, L long) between the experimental measurement and the simulated standard structure. The red dashed lines mark the positions of Mo atomic columns in the experimental data while the black dashed lines indicate the S-Mo-S unit from which the distortion starts.
The first layer of MoS2 was further analyzed in Fig. 3e. Since the atomic structure on the left H region remains identical with the simulated one, there should be no damage or artifact introduced by our microscopy observation. The safeness of our imaging conditions to exclude any e-beam artifacts is also demonstrated by the controlled imaging of pristine monolayer MoS2 under the same conditions as used in the atomic imaging of device contact regions (Supplementary Fig. 13). Both H–T heterophase interfaces are structurally seamless without dangling bonds or defects, where only slight stretching or shrinking of some bond lengths is involved in the distortion. This 1-nm-wide structural change looks similar to the 1 T phase transition, but the Mo–Mo bond angle, length, and interlayer stacking order differ from those of the 1 T phase as compared with the simulated standard H–T interface in Fig. 3f. In specific, the Mo–Mo spacings in the experimental measurement stagger around the equal value in an ideal 1 T phase. The first unit cell in the termination shrinks a bit while the second one on the left elongates. The deviation of atomic positions from standard crystallographic sites as observed here should affect the electronic property through the electron-lattice coupling, which makes the DOS of such semi-metallic nanostructure dispersed away the theoretical work-function value of the ideal crystal. The energy dispersion of DOS thus allows the nearly barrier-free electron transport from the metal Fermi level to the TMDSC conduction band edge as illustrated in the interfacial band diagram of Fig. 1d.
By performing the electron energy-loss spectroscopy (EELS) analysis in this LBD contact region as shown in Supplementary Fig. 3, we found oxygen existing in the distorted MoS2 edge, which is consistent with the proposed formation mechanisms of LBD by the oxygen-substitution-induced bond rearrangements29. On one hand, the oxygen plasma transfers kinetic energy to treated samples to drive the bond distortion; On the other hand, the generated oxygen ions can substitute some chalcogen atoms during the soft O2-plasma treatment and thus locally modifies the bond length, stabilizing the distorted structure. As depicted in Supplementary Fig. 4a, only stretching or shrinking of some bond lengths and angles is involved in the LBD, which in turn balances the size difference between chalcogen and oxygen atoms after the substitution. It is also reported that the incorporation of oxygen species may increase the carrier transmission in the electrical interface with metals29,30. The O2-plasma-induced LBD was further confirmed by micro Raman spectroscopy (Supplementary Fig. 4b). The local distortion of [TM-C6] polyhedra from the trigonal-prismatic coordination to octahedral ones modulates the electronic property into semi-metallicity, boosting the carrier-injection efficiency of electrical contacts and thus device performance as discussed below.
The 3L-MoS2 FET interfaced by the LBD contacts shows excellent performance at both room and cryogenic temperatures. In Fig. 4a, b, linear two-probe output curves, Ids–Vds, can be observed at all gate voltages and well maintained down to 2 K, demonstrating the robust ohmic contact nature. The channel current at 2 K is about 200 times larger than that at 300 K, which suggests a little contribution from the contacts to the total device resistance. In Fig. 4c, the extracted contact resistance at 2 K decreases to around 270 Ω as the back-gate voltage increases, which is 90 Ωμm after considering the geometry factor of device channel. We notice that the quantum limit of the contact resistance is inversely related to the 2D charge carrier density (n), yielding 0.026/√n ≈ 30 Ωμm when n = 1013 cm−2, which suggests that our LBD contact quality is approaching the theoretical limit4. The channel conductance in the inset of Fig. 4d increases steadily by lowering the temperature, reflecting the gradually lifted phonon scattering in the MoS2 channel. The extracted field-effect mobility shows high values of 556 cm2V−1s−1 at room temperature and 23,700 cm2V−1s−1 at 2 K with a phonon-scattering constant of around −1.9, confirming the strong phonon–electron interaction in atomically thin MoS2.
Two-probe Ids–Vds curves at (a) room temperature and (b) 2 K, respectively. c Contact resistance, Rc, extracted from the resistance difference between two-probe and four-probe measurements as the function of gate voltages, where the four-probe resistance is scaled by (frac{{{{{{{rm{L}}}}}}}_{{{{{{rm{out}}}}}}}}{{{{{{{rm{L}}}}}}}_{{{{{{rm{in}}}}}}}}) as described in the Methods section and both resistance values in Ω·μm and Ω units are plotted in the logarithmic scale. It can be seen that the contact resistance depends little on the back gating after the device is fully turned on. The off-state of this device locates below −10 V back-gate voltage due to the natural electron doping of MoS2 as demonstrated in the inset of Fig. 4d. d Temperature-dependent field-effect mobility, μFE, derived from the channel conductance as the inset shows, showing the strong phonon scattering effects of 3L-MoS2 at high temperatures. ({gamma }_{{FE}}) represents the exponential temperature decay constant of the field-effect mobility.
This contact scheme combined with the top-contact geometry as discussed below also works well for monolayer MoS2 as demonstrated in Supplementary Fig. 5. The metal-LBD-MoS2 interfaces effectively lift the carrier-injection barriers in 1L-MoS2 FETs, manifesting high-quality quantum-Hall detection, brilliant subthreshold swings, high field-effect, and Hall mobilities (9900 and 9200 cm2V−1s−1, respectively) at cryogenic temperatures. Such high-performance 1L-MoS2 devices made by the LBD method should facilitate future study on the electron–electron interaction effects at fractional quantum Hall states. The relatively suppressed carrier mobility for 1L-MoS2 may be due to the weaker screening effect of monolayer channels and thus increased scattering by intrinsic impurities, but the effectiveness of our LBD strategy for monolayer TMDSCs is clarified.
Furthermore, we demonstrate the generality of the LBD strategy using 5L-WSe2 in the more common top-contact geometry. The optical image of a typical top-contacted device is shown in Fig. 5a. The top-contact geometry is widely used as it provides a much larger carrier-injection area (as illustrated in Fig. 5b) than the edge-contact scheme. The precise removal of top BN to expose the pristine WSe2 surface is realized by the referenced RIE process as illustrated in Fig. 2. From the low-magnification ADF image of the contact region in Fig. 5c, a uniform top-contact area can be identified, except for some top BN islands that remained due to local thickness differences. After the soft oxygen plasma treatment, the topmost WSe2 layer within the contact window went through the LBD without affecting the layers beneath as shown by the atomic-resolution ADF images of metal-WSe2 electrical junction in Fig. 5d. This LBD metallization exhibits complicated changes of the W–Se bonding without any crystallographic defects (e.g. vacancies or dangling bonds). According to the 2D-Gaussian-fitted W and Se atomic column positions overlaid in the image (Supplementary Fig. 6 for the image-processing details), the newly formed structure turns out to be a mixture of 1 T and 1 T’ octahedral derivatives. Since the nanoscale T/T’-mixed structure does not create defects and thus can be considered as a distorted crystalline structure. Such distorted WSe2 layer acts as a semi-metallic bridge between the metal lead and the pristine WSe2 channel, leading to a nearly barrier-free carrier injection, similar to the cases in MoS2.
a Optical image of a typical 5L-WSe2 FET utilizing LBD contacts. The dash-dot line indicates the cutting position in the source, from which a cross-section membrane was lifted out as illustrated in b. c The low-magnification ADF image of the contact region. The area in the red-dash rectangle is zoomed in as d. d Atomic-resolution ADF image of the WSe2-LBD-metal junction observed along the WSe2 zig-zag direction. The orange dashed lines show the bottom of Ti layer. The LBD-starting region (white dashed rectangle) is analyzed below with the contrast re-surveyed, and the atomic model overlaid to clarify the distorted bonding. The overlaid blue and red dashed lines highlight the lattices of hexagonal WSe2 (H) and octahedral WSe2 (LBD), respectively. e Tow-probe Ids–Vds curves at varied temperatures. f Log-scale plot of field-effect and Hall mobilities as the function of temperatures. ({gamma }_{{FE}}) and ({gamma }_{{Hall}}) represent the exponential temperature decay constants of the field-effect and Hall mobilities, respectively. g Shubnikov de Haas (SdH) oscillations of the longitudinal channel resistance at low magnetic field strength down to ~0.4 T, indicating the high quantum mobility. The solid red line is averaged from the nearest 25 data points and the red arrow indicates the prominent onset position of SdH oscillations at ~0.4 T.
Linear output characteristics are observed across a wide temperature range as shown in Fig. 5e, proving the robust ohmic contact nature. Although the contact resistance of 700 Ωµm is larger than that in the edge-contacted MoS2 due to the inevitable vdW gap in the top-contact geometry (see Supplementary Fig. 7 for extended data from this top-contacted WSe2 FET), high field-effect (μFE ~ 358,000 cm2V−1s−1), Hall (μHall ~ 151,000 cm2V−1s−1) and quantum (μq ~ 25,000 cm2V−1s−1) carrier mobilities are achieved at 0.3 K, as the temperature plots in Fig. 5f and the prominent Shubnikov de Haas (SdH) oscillations in Fig. 5g demonstrate. Although the quantum mobility is a rough estimation from the oscillation onset at low magnetic fields, the derived value should be the lower bound, because the electrical turbulence from both the measurement system and the external environment will bury the real onset of the oscillation amplitude smaller than the noise level. Theoretically, there is μFE > μHall > μq for the same sample and temperature. The field-effect mobility is always higher than the Hall mobility of the same conditions because of μFE = μHall + n (frac{d{mu }_{{Hall}}}{{dn}}), where higher carrier density can screen the impurity scattering and results in (frac{d{mu }_{{Hall}}}{{dn}}) > 0. On the other hand, since the quantum scattering time is always shorter than the transport scattering time, quantum mobility should fall below the corresponding Hall mobility. The quantum mobility is an evaluation of the system’s quality for observing quantum phenomena (see more detailed quantum transport data of such high-mobility WSe2 device in Supplementary Fig. 14). No hysteresis effects were observed when scanning gate voltage forwards and backwards as shown in Supplementary Fig. 7c, which confirm there are no chargeable states caused by the LBD, in consistence with the atomic microscopy observation of no dangling bonds or vacancies formed in the metal-TMDSC junction. Furthermore, the reproducible contact quality after the long-time storage as shown in Supplementary Fig. 7d and the competitive performance of multiple devices with the same contact geometry and different channel thicknesses shown in Supplementary Fig. 8 demonstrate the excellent reproducibility and practicality of our LBD contact strategy for TMDSCs.
The high performance of the electrical interfaces formed by the LBD method is attributed to the octahedral distortion of TMDSCs. Unlike a perfect H–T interface, in which the work functions of bulk 1 T and H phases are mismatched, various sizes of distorted T/T’ derivatives induced by the oxygen plasma are semi-metallic, offering dispersed energy states around its work function. These energy states may play an important role in the orbital hybridization between transition metals and lead atoms, thus enhancing the carrier-injection efficiency. This mechanism is supported by the fact that the polarity of the LBD interfaced FETs is contact-metal dependent. For example, Ti/Au leads can access the conduction band edge (n-type) while Pd leads can access the valence band edge (p-type) of WSe2 (Supplementary Fig. 9). The DOS of the LBD region is distributed along the energy band gap of TMDSCs, easily coupled with different work functions of metal leads. We also measured the resistance-temperature relationship of 1L-MoS2 flake after treated by the same soft oxygen plasma process as that used to fabricate LBD contacts (Supplementary Fig. 10), where the LBD-induced semi-metallicity and the strong electron-phonon coupling are proved. For the standard bulk T–H interface, however, the device polarity is independent of contact metals used12 since the work function of 1 T phase is fixed, resulting in limited accessibility to the energy bands of TMDSCs.
We also conducted transmission line experiments31 on n-type MoS2 using LBD edge contacts, n-type and p-type WSe2 using LBD top contacts as shown in Supplementary Fig. 12. It can be seen that the obtained best contact resistance is 85 ± 15 Ωμm in edge-contacted 3L-MoS2, which is very close to our estimation of 90 Ωμm. For n-type top-contacted WSe2, the contact resistance falls within 100–200 Ωμm across ranges of carrier densities and temperatures. As a complementary measurement, in Supplementary Fig. 15, we demonstrate the contact resistance extraction of LBD-contacted MoS2 and WSe2 devices by comparing the two- and four-terminal resistance, showing consistent contact resistance values at room temperature. In principle, the contact resistance is dependent on the carrier density and the temperature. The higher carrier density and lower temperature lead to the better contact resistance, which may be explained by the fact that the impurity scattering in channels or contact interfaces can be screened by clouded carriers and suppressed by lowered temperature. This correlation in top-contacted p-type WSe2 is more prominent.
In conclusion, we demonstrate a proof-of-concept LBD contact strategy by the soft oxygen plasma treatment, which is flexible for both edge- and top-contact fabrication schemes, to construct high-quality electrical junctions between metal leads and different TMDSCs, down to their monolayer limit. The excellent performance of such electrical contacts is structurally understood by the cross-section electron microscopy observation of metal-semiconductor junctions from practical devices. By exploiting such high-quality contacts, we have achieved robust ohmic behaviors, the low contact resistance (down to 90 Ωµm in 3L-MoS2), the high mobilities (up to 358,000 cm2V−1s−1 in 5L-WSe2) and prominent transport characteristics. Since the electrical contact quality at cryogenic temperatures has been considered as the main factor constraining the study of unconventional quantum transport properties in TMDSCs, our LBD contact strategy should facilitate high-quality TMDSC device fabrication for quantum physics study. Importantly, this method is fully compatible with the clean-room processes for scalable electrode integration and may shed light on the future vdW device design.
TMDSC crystals were bought from the website www.2dsemiconductors.com while the hexagonal BN (grade A1) was bought from the website www.hqgraphene.com.
The sandwich structure of top BN (5–8 nm), few-layer 2H-MoS2/WSe2, and bottom BN (12–20 nm) was assembled by the dry pickup-transfer technique in a glove box. Following the electron-beam lithography patterning of a thin poly(methyl methacrylate) (PMMA, A5) mask using Raith eLiNE, the heterostructure was first shaped into Hall-bar structure by the reactive ion etching (RIE) in STS Pro using the gas mixture of CHF3 and O2 (40:4 sccm). Repatterning a PMMA mask then defined the contact windows and a reference area for the referenced RIE as illustrated in Fig. 2. Before the deposition of metal leads, the TMDSCs were exposed to the pure oxygen-plasma flow for around 10 s in a soft-landing manner, which was realized by paralleling the electrostatic field along the sample surface, reducing the plate bias and lowering the input power. The non-destructive metal deposition22, i.e. critically high vacuum of 3 × 10−7 Torr and slow deposition rate of 0.2 Å/s, was performed by Peva 450E right after the oxygen plasma treatment to minimize the influence from the metal deposition process and seal the contact windows.
The etching and plasma treatment were performed using the RIE system in a combination of parallel plate and inductively coupled plasma (ICP), model STS Pro, under the conditions as shown in Table 1. The ICP can generate a high-density source of ions while the separate RF bias in parallel plate can create directional electric fields near the substrate. In our soft oxygen plasma treatment, the vertical substrate bias is tuned to ~0 to reduce the kinetic energy of oxygen ions for complete reaction with samples and also to avoid possible etching effects.
The plasma treatment is reproducible and practical once suitable conditions are set up. As shown in Supplementary Fig. 8a, the contact resistance and field-effect mobility of multiple back-gated 3L-MoS2 and 5L-WSe2 FETs using the LBD contacts show similar high quality. The device deviation is reasonable considering the fabrication error by human handling and laboratory facilities. We notice that WSe2 FETs show a larger device-to-device variation, which may be attributed to the higher mixed state of octahedral derivatives in LBD-treated WSe2 than the situation of MoS2.
The DC Ids–Vds curves were measured in the two-probe configuration using Keithley 6430 while the channel conductance (σ) and magneto-transport measurements were conducted in the four-probe configuration using lock-in techniques (Stanford Research 830 as the amplifier and DS 360 as the function generator). The cryogenic station from Oxford Instruments was used to provide cryogenic temperatures down to 1.4 K and magnetic fields up to 15 T. A home-modified He3 holder provides a stable 0.3 K environment for ~24 h per regeneration.
Different types of carrier mobilities were calculated to assess the contact performance, including field-effect, Hall and quantum mobilities. The field-effect mobility (μFE) values were obtained according to μFE (=frac{1}{C}frac{Delta sigma }{Delta {V}_{g}}), where C is the gate capacitance (from serially-connected capacitors of the 300 nm SiO2 and the 12–20 nm bottom BN layer for back-gated devices), which was accurately determined by the Hall effect measurements of carrier density versus gate voltage relationship. The (frac{Delta sigma }{Delta {V}_{g}}) is the slope of channel conductance (σ (=frac{{GL}}{W}), where G is the four-probe conductance, L is the channel length and W is the channel width of inner probes) versus gate voltage at the linear region. The Hall mobility (μHall) values were obtained according to μHall = (frac{sigma }{{ne}}), where n is the carrier density derived from the Hall coefficient, e is the elementary charge. The quantum mobility (μq) value was derived from the lowest perpendicular magnetic field strength Bq where SdH oscillations onset, as μq = (frac{1}{{B}_{q}}). The exponential temperature decay of both field-effect and Hall mobilities follows Tγ, where γ indicates the phonon scattering strength.
The contact resistance was extracted from the resistance difference between two-probe and four-probe measurements according to 2 * Rc = (R2p − (frac{{L}_{{out}}}{{L}_{{in}}})R4p) * W, where R2p and R4p are the two-probe and four-probe resistance, respectively; Lout and Lin are the distance of outer probe pair and inner probe pair in the four-probe configuration, respectively.
Focused ion beam (FIB) techniques using FEI Helios G4 UX were applied to prepare the cross-section membranes from FET contact sites, after electrical measurements. Before ion milling processes, a low-energy (2 kV) electron beam was used to identify the exact contact positions and deposit 500-nm-thick Pt protecting straps on the top of metal leads. Then thicker Pt protecting straps (1.5 μm thick) were deposited using the ion beam. After lifting out a 1-μm-thick plate from the chosen contact site to a copper finger, step-by-step thinning processes using 30, 5, 2, 1, and 0.5 kV ion beams well minimized the beam damage to the 2D-material heterostructures. Finally, an ex-situ 500 V argon-ion beam shower of 30 s was used to further clean both membrane surfaces. According to the low-loss electron energy-loss spectroscopy (EELS), the typical sample thickness at the contact interface is 12.3 ± 2.5 nm, which guarantees atomic-resolution imaging and elemental mapping at 60 kV acceleration voltage.
JEOL JEM ARM 200 F (ACCELARM) equipped with a cold field-emission gun and the ASCOR fifth-order probe corrector was utilized for the aberration-corrected scanning transmission electron microscopy (ACSTEM) study of the contact interface at atomic resolution under 60 kV acceleration voltage. Imaging and spectroscopy were performed using 32 mrad convergence semi-angle and 24–60 pA probe current for the optimal information transfer and minimal electron irradiation. Our imaging conditions of low acceleration voltage of 60 kV, low electron irradiation dose of ~7.5–20.0 Me nm−2, and room temperature remain far away from the threshold to cause electron-induced structure change32. The collection semi angles for annular dark field (ADF) imaging was set to 68–200 mrad and the Gatan Enfinium spectrometer was used for the acquisition of energy-loss spectra under the dual EELS mode.
The atomic positions in model drawings of Fig. 3e and Fig. 5d were extracted by the 2D-Gaussian fitting of normalized intensities of atomic columns in the HAADF images. We show the data-processing workflow and distortion-analysis examples in Supplementary Fig. 6. The method can provide picometer precision for the fitted atomic positions when using an aberration-corrected STEM. Based on the extracted atomic positions, the LBD of oxygen-plasma-treated MoS2 and WSe2 can be identified by bond-length/angle variations unit cell by unit cell in comparison to the simulation of standard structures.
Multislice codes by Earl J. Kirkland were used for the simulation of atomic-resolution ADF images to handle the dynamical scattering processes between matter and transmitted electrons33. 2H, 1 T, and 1 T’ structure files were downloaded from the American Mineralogist Crystal Structure Database. An electron probe of experimental conditions was focused on the crystal surface and the scattered electrons within 68–200 mrad collection semi angles were integrated. Twenty frozen phonon configurations were applied to represent the thermal diffuse scattering effects at room temperature. The effective source size effect was included by convolving simulated images with a 2D-Gaussian function of 0.8 Å FWHM.
The plane-wave pseudopotential method implemented in the Quantum ESPRESSO package (version 6.1)34 was used to calculate electronic structures. The SG15 Optimized Norm-Conserving Vanderbilt (ONCV) pseudopotentials were used here35,36. Fully relativistic pseudopotentials were employed in the calculations with spin-orbital coupling37. The kinetic energy cutoff for plane waves was 60 Ry. The convergence thresholds for energy, force, and stress were 10−5 Ry, 10−4 Ry/Bohr, and 50 MPa, respectively. The multilayer structures were obtained from full relaxation with the van der Waals functional optB8838. PBE exchange-correlation functional was adopted to calculate electronic structures39.
Relevant data supporting the key findings of this study are available within the article and the Supplementary Information files. All raw data generated during the current study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Butler, S. Z. et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013).
Article CAS Google Scholar
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Article CAS Google Scholar
Novoselov, K., Mishchenko, A., Carvalho, A. & Neto, A. C. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Article CAS Google Scholar
Jena, D., Banerjee, K. & Xing, G. H. 2D crystal semiconductors: Intimate contacts. Nat. Mater. 13, 1076–1078 (2014).
Article ADS CAS Google Scholar
Allain, A., Kang, J., Banerjee, K. & Kis, A. Electrical contacts to two-dimensional semiconductors. Nat. Mater. 14, 1195–1205 (2015).
Article ADS CAS Google Scholar
Schulman, D. S., Arnold, A. J. & Das, S. Contact engineering for 2D materials and devices. Chem. Soc. Rev. 47, 3037–3058 (2018).
Article CAS Google Scholar
Tung, R. T. Chemical bonding and Fermi level pinning at metal-semiconductor interfaces. Phys. Rev. Lett. 84, 6078 (2000).
Article ADS CAS Google Scholar
Kim, C. et al. Fermi level pinning at electrical metal contacts of monolayer molybdenum dichalcogenides. ACS Nano 11, 1588–1596 (2017).
Article CAS Google Scholar
Perera, M. M. et al. Improved carrier mobility in few-layer MoS2 field-effect transistors with ionic-liquid gating. ACS Nano 7, 4449–4458 (2013).
Article CAS Google Scholar
Chuang, H.-J. et al. Low-resistance 2D/2D ohmic contacts: a universal approach to high-performance WSe2, MoS2, and MoSe2 transistors. Nano Lett. 16, 1896–1902 (2016).
Article ADS CAS Google Scholar
Zheng, X. et al. Patterning metal contacts on monolayer MoS2 with vanishing Schottky barriers using thermal nanolithography. Nat. Electron. 2, 17–25 (2019).
Article ADS CAS Google Scholar
Kappera, R. et al. Phase-engineered low-resistance contacts for ultrathin MoS2 transistors. Nat. Mater. 13, 1128–1134 (2014).
Article ADS CAS Google Scholar
Cho, S. et al. Phase patterning for ohmic homojunction contact in MoTe2. Science 349, 625–628 (2015).
Article ADS CAS Google Scholar
Zhu, J. et al. Argon plasma induced phase transition in monolayer MoS2. J. Am. Chem. Soc. 139, 10216–10219 (2017).
Article CAS Google Scholar
Wang, J. et al. High Mobility MoS2 transistor with low Schottky barrier contact by using atomic thick h‐BN as a tunneling layer. Adv. Mater. 28, 8302–8308 (2016).
Article CAS Google Scholar
Cui, X. et al. Low-temperature ohmic contact to monolayer MoS2 by van der Waals bonded Co/h-BN electrodes. Nano Lett. 17, 4781–4786 (2017).
Article ADS CAS Google Scholar
Cui, X. et al. Multi-terminal transport measurements of MoS2 using a van der Waals heterostructure device platform. Nat. Nanotechnol. 10, 534–540 (2015).
Article ADS CAS Google Scholar
Liu, Y. et al. Toward barrier-free contact to molybdenum disulfide using graphene electrodes. Nano Lett. 15, 3030–3034 (2015).
Article ADS CAS Google Scholar
Liu, Y., Stradins, P. & Wei, S.-H. Van der Waals metal-semiconductor junction: weak Fermi level pinning enables effective tuning of Schottky barrier. Sci. Adv. 2, e1600069 (2016).
Article ADS Google Scholar
Liu, Y. et al. Approaching the Schottky–Mott limit in van der Waals metal-semiconductor junctions. Nature 557, 696–700 (2018).
Article ADS CAS Google Scholar
Jung, Y. et al. Transferred via contacts as a platform for ideal two-dimensional transistors. Nat. Electron. 2, 187–194 (2019).
Article Google Scholar
Wang, Y. et al. Van der Waals contacts between three-dimensional metals and two-dimensional semiconductors. Nature 568, 70–74 (2019).
Article ADS CAS Google Scholar
Fallahazad, B. et al. Shubnikov–de Haas oscillations of high-mobility holes in monolayer and bilayer WSe2: Landau level degeneracy, effective mass, and negative compressibility. Phys. Rev. Lett. 116, 086601 (2016).
Article ADS Google Scholar
Liu, G.-B., Xiao, D., Yao, Y., Xu, X. & Yao, W. Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 44, 2643–2663 (2015).
Article CAS Google Scholar
Yang, Z. et al. A Fermi‐level‐pinning‐free 1D electrical contact at the intrinsic 2D MoS2-metal junction. Adv. Mater. 31, 1808231 (2019).
Article Google Scholar
Fang, Y. et al. Structure re‐determination and superconductivity observation of Bulk 1 T MoS2. Angew. Chem. 130, 1246–1249 (2018).
Article ADS Google Scholar
Viswanathan, M. et al. Influence of lattice distortion on the Curie temperature and spin–phonon coupling in LaMn0.5Co0.5O3. J. Phys.: Condens. Matter 22, 346006 (2010).
CAS Google Scholar
Nguyen, T. H. et al. Raman spectroscopic evidence of impurity‐induced structural distortion in SmB6. J. Raman Spectrosc. 50, 1661–1671 (2019).
Article ADS CAS Google Scholar
Jadwiszczak, J. et al. Oxide-mediated recovery of field-effect mobility in plasma-treated MoS2. Sci. Adv. 4, eaao5031 (2018).
Article ADS Google Scholar
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Article ADS CAS Google Scholar
Shen, P.-C. et al. Ultralow contact resistance between semimetal and monolayer semiconductors. Nature 593, 211–217 (2021).
Article ADS CAS Google Scholar
Lin, Y.-C., Dumcenco, D. O., Huang, Y.-S. & Suenaga, K. Atomic mechanism of the semiconducting-to-metallic phase transition in single-layered MoS2. Nat. Nanotechnol. 9, 391–396 (2014).
Article ADS CAS Google Scholar
Kirkland, E. J. Advanced Computing in Electron Microscopy. (Springer Science & Business Media, 2010).
Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys.: Condens. Matter 29, 465901 (2017).
CAS Google Scholar
Hamann, D. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).
Article ADS Google Scholar
Schlipf, M. & Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Computer Phys. Commun. 196, 36–44 (2015).
Article ADS CAS Google Scholar
Scherpelz, P., Govoni, M., Hamada, I. & Galli, G. Implementation and validation of fully relativistic GW calculations: spin-orbit coupling in molecules, nanocrystals, and solids. J. Chem. Theory Comput. 12, 3523–3544 (2016).
Article CAS Google Scholar
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys.: Condens. Matter 22, 022201 (2009).
ADS Google Scholar
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Article ADS CAS Google Scholar
Download references
The work is partially supported by the National Key R&D Program of China (2020YFA 0309600), the Hong Kong Research Grants Council (Projects No. AoE/P-701/20, C7036-17W, 16305919, 16303720 and C6025-19G), and the William Mong Institute of Nano Science and Technology. C.C. thanks the funding support from the National Natural Science Foundation of China (Grants No. 91963129 and 51776094).
These authors contributed equally: Xiangbin Cai, Zefei Wu.
Department of Physics and Center for Quantum Materials, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
Xiangbin Cai, Zefei Wu, Xu Han, Yong Chen, Shuigang Xu, Jiangxiazi Lin, Tianyi Han, Pingge He, Xuemeng Feng, Liheng An, Run Shi, Jingwei Wang, Zhehan Ying, Yuan Cai, Junwei Liu, Ding Pan & Ning Wang
Department of Chemistry, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
Xu Han & Ding Pan
Department of Materials Science and Engineering, Southern University of Science and Technology, Shenzhen, 518055, China
Yong Chen, Run Shi, Jingwei Wang & Chun Cheng
Department of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, 518055, China
Mengyuan Hua
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
N.W. conceived and directed the project. Z.W., X.C., Y.Ch., S.X., J.Lin., T.H., X.F., and L.A. conducted the device fabrication and electrical measurements. X.C. performed the FIB sample preparation and ACSTEM characterization. X.H., J.Liu., and D.P. carried out the DFT calculations. R.S., P.H., and J.W. grew the MoS2 monolayer crystals. Z.Y. and Y.Ca. provided the technical support of TEM facilities. M.H. and C.C. assisted with electrical measurements. X.C. and N.W. wrote the paper. All authors participated in the data analysis, result discussion, and manuscript preparation.
Correspondence to Ning Wang.
The authors declare no competing interests.
Nature Communications thanks Hongzhou Zhang and the other anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and permissions
Cai, X., Wu, Z., Han, X. et al. Bridging the gap between atomically thin semiconductors and metal leads. Nat Commun 13, 1777 (2022). https://doi.org/10.1038/s41467-022-29449-4
Download citation
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-29449-4
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Nature Communications (2024)
Nature Communications (2024)
Nano Research (2024)
Frontiers of Physics (2023)
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Advertisement
© 2024 Springer Nature Limited
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.