Electrical control of transient formation of electron-hole coexisting system at silicon metal-oxide-semiconductor interfaces | Communications Physics – Nature
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
Advertisement
Communications Physics volume 6, Article number: 316 (2023)
1283
8
Metrics details
Recent observations of macroscopic quantum condensation using electron-hole (e-h) bilayers have activated the research of its application to electronics. However, to the best of our knowledge, no attempts have been made to observe the condensation in silicon, the major material in electronics, due to the lack of technology to form closely-packed and uniform bilayers. Here, we propose a method to meet such requirements. Our method uses the transient response of carriers to a rapid gate-voltage change, permitting the self-organized bilayer formation at the metal-oxide-semiconductor interface with an e-h distance as small as the exciton Bohr radius. Recombination lifetime measurements show that the fast process is followed by a slow process, strongly suggesting that the e-h system changes its configuration depending on carrier density. This method could thus enable controlling the phase of the e-h system, paving the way for condensation and, ultimately, for low-power cryogenic silicon metal-oxide-semiconductor devices.
Electron-hole (e-h) coexisting systems form in semiconductors in various phases: plasma, liquid, and gas (excitons), depending on the temperature and density, due to the Coulomb interaction. These systems have attracted continuous attention from the viewpoint of many-body physics1,2,3,4,5,6.
In particular, the progressive development of the physics and technologies for the e-h bilayers in compound semiconductors7,8,9,10, and more recently, in the two-dimensional (2D) materials, such as transition-metal dichalcogenides11,12,13,14,15 and graphene16,17,18, has activated the research on the macroscopic quantum condensations, i.e., Bose-Einstein condensation (BEC), Bardeen-Cooper-Schrieffer states, and their crossover. Stimulated by these studies7,8,9,10,11,12,13,14,15,16,17,18, applications of the quantum condensation to optoelectronic and electronic devices have also been intensively considered19,20,21,22,23,24. One example is “bilayer pseudospin field-effect transistor (FET)”19,23, whose operation is based on the discovery that the recombination rate drastically increases when the e-h bilayer exhibits BEC8. Sun et al. recently showed that the condensation bilayer state can be used as a device that works like a Josephson junction, using a similar mechanism21. Another idea is to use the “perfect drag”, taking place under the BEC conditions, which could be used to develop a DC current transformer24.
Considering the application to electronics, especially to rapidly developing cryogenic electronics based on the complementary metal-oxide-semiconductor (CMOS) technologies25,26,27, research on these phenomena in silicon (Si) becomes critical. The e-h coexisting system in Si has been investigated from the viewpoint of clarifying the basic properties of the e-h system in semiconductors28,29,30,31,32,33,34. However, research aiming at the realization of the condensation is not active. Only a few papers35,36,37 have so far reported e-h bilayers in Si, in which adjacent electron and hole layers were formed at the front and back interfaces of thin silicon-on-insulator (SOI) layers for the purpose of observing frictional drag38.
The main cause of this stagnation is the concern that the thickness fluctuation of thin SOI layers causes inhomogeneous density profiles of electrons and holes, which could fatally block the condensation of excitons in the e-h bilayer39. The state-of-the-art fully-depleted (FD) SOI technology achieves a uniform Si film with the standard deviation of thickness fluctuation being about 0.4 nm40. This is remarkable, but still one order of magnitude lager than those of the 2D materials on boron nitride film41. On the other hand, for the silicon dioxide (SiO2)/Si interface itself, the effect of the roughness is recognized to be minor (if the charge density is low), and thus this interface has been the playground for the research of strongly interacting 2D electron systems, without the annoyance of the potential disorder caused by the interface roughness42,43,44. Therefore, in order to avoid the thickness-fluctuation problem of the SOIs, while still taking advantage of the high quality of the SiO2/Si interface, we propose here a method to form the e-h system at the single SiO2/Si interface of bulk (non-SOI) MOSFETs.
In this Article, we experimentally investigate the transient electrical formation of the e-h coexisting system in such bulk MOSFETs. The method uses the response of carriers to a rapid gate-voltage change under low temperature conditions; electrons are induced from the source/drain by a gate voltage pulse, while holes are confined in a potential well formed at the interface. We measured the e-h recombination current generated by repetitive pulses, and analyzed it as a function of the gate-pulse parameters. We demonstrate that the e-h system is formed at low temperatures, below about 30 K, and that the densities of the electrons and holes can be independently controlled by the amplitude and the base voltage of the pulse, respectively. Most importantly, we found that the introduced electrons are located in close proximity to the interface hole layer, at a distance on the order of nanometers, comparable to the Bohr radius of excitons in Si, revealing the self-organized formation of the e-h bilayer with a strong Coulomb coupling. In addition, the recombination lifetime measurements indicate that the fast process is followed by a slow process, suggesting that the introduced electrons change its configuration from plasma (Fermi gas) to the exciton.
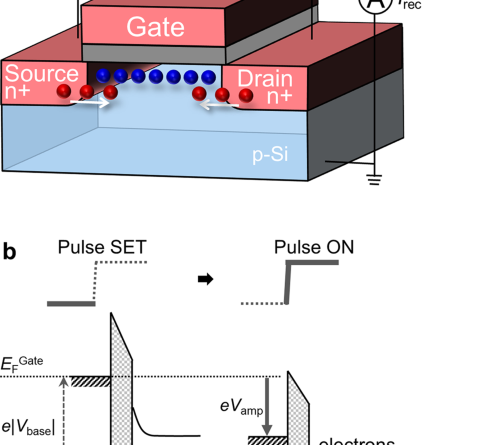
Figure 1 explains the method. Figure 1a shows the setup for n-channel MOSFETs. While the source/drain and the substrate terminals are grounded, we apply a pulse voltage to the gate with the base voltage Vbase and the amplitude Vamp, and measure the averaged current Irec flowing between the source/drain and the substrate. Figure 1b shows the energy band diagrams during the pulse sequence. As shown in the left diagram, we first set the Vbase to a negative value. The Fermi level of the gate EFGate then increases by (−e)Vbase, and holes are accumulated at the interface. We call this step “Pulse SET”. We next rapidly raise the gate voltage by Vamp so that the EFGate decreases by eVamp. We call this step “Pulse ON” (see the right diagram). If the temperature is low enough, the accumulated holes are expected to remain at the interface owing to the suppression of the thermal emission from the accumulation potential well. In such a case, with a sufficiently large value of Vamp, electrons can be introduced from the source/drain to the hole-accumulated interface, resulting in the coexistence of electrons and holes.
a Setup for formation and measurements of electron-hole coexisting system. A rapid voltage change under low temperature conditions induces electrons from the source/drain (red circles) while the substrate holes remained at the interface (blue circles). The recombination current Irec flows between the grounded source/drain and substrate. The inset shows the definition of the base and amplitude of the gate pulse. b Energy band diagrams for the hole accumulation (Pulse SET) and for the electron injection (Pulse ON). EFSD,Sub denotes the Fermi level of the source/drain and substrate, both of which are grounded in the present experiments (EFSD,Sub = 0), while EFGate denotes the Fermi level of the gate. At the “Pulse SET” stage, by applying the Vbase (which is negative) to the gate, EFGate becomes larger than EFSD,Sub by the amount of (–e)Vbase (= e|Vbase|), and holes are accumulated at the interface. At “Pulse ON” stage, EFGate decreases by (–e)Vamp, as indicated by the downward arrow, and electrons are introduced from the source/drain. Note that the right diagram is drawn for the case where |Vbase| – Vamp > 0 because the measurements for the main results (Irec – Vbase characteristics) were mostly done under this condition. With this condition, Nh0 > Ne holds. In such a case, the net charge Q at the interface is positive, i.e., Q = eNh0 + (–e)Ne > 0, and thus the electric field in the oxide is kept negative.
Figure 1b-right shows the expected potential profile when electrons are being introduced at the “Pulse ON” stage. Positive charges (of the holes) cause a steep downward-convex potential profile at the interface (Fig. 1b-left) like p-channel MOSFETs. On the other hand, negative charges (of the electrons) create an upward-convex potential profile like n-channel MOSFETs. Electrons are expected to be trapped at the potential pocket created by the combination of these two profiles, resulting in the bilayer-like charge profile.
The resultant e-h coexistence persists until the electrons and holes annihilate by recombination. Owing to the indirect-bandgap nature of Si, the recombination time is expected to be long, e.g., on the order of μs for the case of exciton recombination45. This time scale is much longer than the typical time constants important for e-h systems, such as the relaxation time due to the Coulomb interaction and exciton formation time, which are less than 1 ps46,47 and 1 ns47,48, respectively. Therefore, the present e-h system can be regarded as being under quasi-equilibrium, with the electron and hole densities well defined within the time scale of interest. Thus, it can be anticipated that it provides a good experimental host to investigate the properties and dynamics of the e-h system at Si MOS interfaces for future research.
Although, as we mentioned above, the recombination itself is the obstacle for the formation of a stable e-h system, we rather utilize it in this study for observing the e-h coexistence. We should mention here that similar transient experiments have been made focusing on the depletion-layer formation and on the possibility of the e-h plasma formation49,50,51. However, in these pioneering studies, the analysis ignored the e-h recombination process, and neither direct observation of the e-h coexistence, evaluation of the electron and hole densities, nor the estimation of the relative placement of electrons and holes have been done. We hereafter show that the recombination current conveys such important information about the e-h system. We should also mention that the present e-h coexistence due to the rapid voltage swing is relevant to the phenomenon called the “geometric effect”52,53 in the charge pumping (CP) process54, which is known as a limiting factor for the CP operating at high frequencies. The present method can be regarded as employing this phenomenon in a controlled way to form the closely-packed e-h bilayer.
The experiment we performed is the following. At “Pulse SET” stage, we wait a sufficiently long time, on the order of milliseconds, until the system reaches equilibrium, i.e., until the density of the accumulated holes Nh reaches the one determined by the accumulation gate-capacitance (per unit area) Cg,h for the hole layer, as Nh = Nh0 (≡ − Cg,h (Vbase – Vacc)/e), where e is the elementary charge and Vacc is the threshold voltage for the accumulation. We next made a rapid rising of the pulse voltage by Vamp, with the rising time on the order of 10 ns, resulting in the electron introduction. We then keep the voltage at Vbase + Vamp for a time interval tON. We repeat this process and measure the generated recombination current Irec flowing between the grounded source/drain and substrate (see Fig. 1a). With A and f being the channel area and pulse frequency, Irec is expressed by Irec = ANrecef, where Nrec is the density of the e-h pairs recombined in one cycle of the pulse. The period tON of the “Pulse ON” stage was set to be sufficiently long, on the order of milliseconds, so that all the recombination events are completed within one cycle of the gate pulse.
Exception is the measurement for the recombination lifetime, where tON was varied in the range between 10 ns to 100 μs in order to evaluate it. In addition, to support the data of the recombination lifetime, we also performed the real-time monitoring of the recombination current using a high-speed current amplifier.
The measurements were conducted at 8 K except for the measurements for temperature T dependence, where T was varied between 8 and 50 K.
For the measurements, n-channel MOSFETs fabricated on a Si (100) substrate were used. The channel length/width and gate-oxide thickness are, respectively, 50/500 μm and 30 nm. The substrate impurity (boron) concentration is on the order of 1015 cm−3. The basic characteristics of the MOSFET measured at 8 K can be found in the Supplementary Information. The field effect mobility exceeds 10,000 cm2V−1s−1 (see Supplementary Note 1), ensuring that the channel interface is of high quality. We also observed the metal-insulator transition with the critical electron density of 2 × 1011 cm−2 (see Supplementary Notes 2 and 3). This observation also ensures the high-quality of the interface, and it is expected that the potential disorder caused by the impurities is minor in the present measurements.
Figure 2 shows Irec (left axis) and Nrec (right axis) as a function of Vbase. The value of Vamp was fixed at 4 V. (The other parameters of the pulse are described in the caption of Fig. 2.) One can see that the characteristics are divided into three Vbase regions.
The density of recombined e-h pairs Nrec converted from Irec is shown on the right axis. The red dashed line indicates the saturated level of Irec and Nrec. The blue dashed line indicates the slope expected from the accumulation-capacitance model. The measured Nrec is slightly larger than the dashed blue line in the Vbase range of −3.4 V < Vbase < −1 V, which is due to the recombination of electrons with the holes trapped at the interface defects (see Methods section). Band diagrams in the upper part of the figure show the recombination process for four different Vbase values. The red and blue circles, respectively, represent introduced electron density Ne and initial hole density Nh0, while the dashed arrows represent Nrec. The pulse form is shown in the left-bottom corner. The pulse rising slope was set at 10 nsV−1, corresponding to the rising time tR of 40 ns for amplitude Vamp = 4 V. (The falling time, which is unimportant in this study, was set at 50 ns.) The frequency f and the duty cycle of the pulse are, respectively, 500 Hz and 50%. The resultant hold times, tSET and tON, for the “Pulse SET” and “Pulse ON” stages, are both approximately 1 ms.
For Vbase ≳ −1.6 V, Irec and Nrec are negligibly small. This was ascribed to no hole accumulation layer being formed at the “Pulse SET” stage, i.e., Nh0 = 0. For the Vbase window, −4 V ≲ Vbase ≲ −1.6 V, Irec and Nrec increase nearly linearly with decreasing Vbase. The blue dashed line in the figure indicates the line Nrec = Nh0 (= − Cg,h (Vbase – Vacc)/e), with Vacc = –1.6 V. For this line, we used Cg,h (accumulation gate-capacitance) = 116 nFcm−2, which was obtained from CV measurements. One can see that the line traces well the experimental data. In addition, the value of Vacc (= –1.6 V) was found to be consistent with the expected value of the threshold voltage for the accumulation-layer formation. Therefore, we concluded that, in this Vbase range, the e-h recombination is dominated by Nh0 (Nh value set at the “Pulse SET” stage) so that Nrec = Nh0. (Note that the analysis of the slope and of Vacc was found to require careful consideration of the recombination of holes trapped at the interface defects, and the details of the analysis can be found in the Methods section.)
The above analysis suggests, in turn, that Ne > Nh0 (= Nrec), where Ne is the density of the introduced electrons (see the upper-right diagram in Fig. 2). That means that all the holes are recombined with the introduced electrons (and residual electrons are turned back to the source/drain at the next “Pulse SET” stage).
For Vbase smaller than about −4 V, on the other hand, Nrec saturates at a nearly constant value. We expect that this is because Ne did not reach Nh0 as Nh0 had a large value due to the negatively large Vbase. In such a case, Nrec should be limited by Ne, i.e., Nrec = Ne (see the upper-left diagram in Fig. 2). In order to confirm this expectation, we performed the same measurements using Vamp as a parameter. The results are shown in Fig. 3a. As expected, the saturation value of Nrec increases with increasing Vamp. This is because a larger Vamp causes larger Ne. In Fig. 3b, we plot the saturated Nrec at Vbase = −10 V as a function of Vamp. One can see that Nrec linearly increases with a distinct threshold at Vamp = 1.2 V, which is denoted by Vamp,th in the figure.
a Irec (left axis) and density of recombined e-h pairs Nrec (right axis) as a function of pulse base voltage Vbase for Vamp values ranging from 1 to 6 V at T = 8 K. The pulse conditions are the same as those for Fig. 2, except for the Vamp variation. The blue dashed line indicates the slope expected from the accumulation-capacitance model. The hatched region indicates the current component caused by the recombination of electrons with the holes trapped at the interface defects. The data point marked by blue circle (Vbase = −10 V and Vamp = 6 V) indicates the measurement conditions for the recombination lifetime measurements. b Nrec–Vamp characteristics for Vbase = −10 V marked by the filled circles in a. The red dashed line shows the fitting line to the experimental data. A threshold Vamp of Nrec denoted by Vamp,th (= 1.2 V) is marked by the arrow. Band diagrams in the inset show the recombination process for two different Vamp values. The red and blue circles, respectively, represent the introduced electron density Ne and initial hole density Nh0, while the dashed arrows represent Nrec. c Band diagram, explaining accumulation layer capacitance Cg,h and electron layer capacitance Cg,e. ΔC, εSi, and d are, respectively, the additional capacitance, the dielectric constant of Si, and the distance between electron and hole layers. d d (left axis) and ΔC-1 (right axis) as a function of Vbase. For the upper horizontal axis, the Nh0 is converted from Vbase. The uncertainty of the results indicated by the error bars mostly arises from the process for determining Cg,h, i.e., the slope represented by the blue dashed line in a.
The linear dependence of the saturated Nrec on Vamp indicates that Ne can be well controlled by the capacitive coupling to the gate. The obtained eVamp,th (= 1.2 eV) is close to the band-gap energy of Si at low temperatures, 1.17 eV55. This agrees with our expectation. As represented by the blue dashed lines in Figs. 2 and 3a, Nrec equals to Nh0 (the initial value of Nh) in the linear region. This is the important manifestation that the emission (leakage) of holes from the accumulation potential well is negligibly small during the “Pulse ON” stage. This means that the accumulated holes can be regarded as fixed positive charges, which shift the threshold voltage for the electron channel in the negative gate-voltage direction. In such a case, the value of Vamp required for the electron channel formation should correspond to the bandgap energy irrespective of the value of Nh0 because, at the “Pulse SET” stage, the Fermi level lies (or is pinned) at around the valence-band edge due to the hole accumulation-layer formation.
We then discuss the slope in Fig. 3b. Different from the blue dashed lines in Figs. 2 and 3a, where the slope was fixed at Cg,h/e based on the accumulation-capacitance model, the red dashed line in Fig. 3b is the one obtained by fitting. The line is expressed by Nrec = Cg,e (Vamp – Vamp,th)/e and, in this case, Cg,e is the fitting parameter. We obtained Cg,e = 109 nFcm−2. The Cg,e can be expressed as Cg,e−1 = Cg,h−1 + ΔC−1, where ΔC is the additional capacitance (see Fig. 3c). Using Cg,h = 116 nFcm−2 and the dielectric constant of Si, εSi = 11.9ε0, where ε0 is the dielectric constant in vacuum, we obtained ΔC = 1.7 μFcm−2, corresponding to the length scale d = 6 nm, in the form of ΔC = εSi/d. This estimation suggests that the center of mass of the introduced electrons or the peak of the electron wave-function is positioned in close proximity to the hole layer, at a distance on the order of the Bohr radius rB (= 4 nm) of excitons in Si28.
We made the same analysis for various Vbase ranging from −4 V to −10 V. Figure 3d shows the estimated ΔC−1 (right axis) and corresponding d (left axis) as a function of Vbase (bottom axis) and corresponding Nh0 (top axis). As you can see, the value of d decreases with decreasing Vbase, i.e., with increasing Nh0, indicating that the placement of introduced electrons relative to the hole layer is dominated by the strength of the Coulomb interaction with the holes. Notice that the uncertainty of the results indicated by the error bars mostly arises from the process for determining Cg,h, i.e., the slope represented by the blue dashed line in Fig. 3a.
We next discuss the T dependence. Figure 4a shows the Nrec – Vbase characteristics for T ranging from 8 to 50 K. In Fig. 4b, we plot the saturated Nrec at Vbase = −10 V as a function of T. When T increases, the saturated Nrec starts to decrease at around T = 30 K. In accordance with this decrease, the slope of the Nrec – Vbase line in the Vbase range −4 V ≲ Vbase ≲ −1.6 V becomes gentler (Fig. 4a). These results indicate that holes are emitted from the accumulation layer during the “Pulse ON” stage, and the emission rate increases as T increases. T = 30 K corresponds to the energy broadening 3.5 kT of the Fermi-Dirac distribution of 9.1 meV, where k is the Boltzmann constant. This value is comparable to the barrier height of the ground subband level of the hole accumulation layer (a few tens of meV56,57). This is an implication that the leakage of the holes is caused by the thermal emission from the potential well of the accumulation layer (see potential diagram in Fig. 4b). We mention that at 50 K all the holes in the accumulation layer set at the “Pulse SET” stage were emitted before the electron introduction. Therefore, no Nrec was generated except for the additional component (the hatched region in the figure) originating from the recombination of holes trapped at the interface defects. (For the effects of the interface defects, see the Methods section).
a Nrec–Vbase characteristics for temperatures T ranging from 8 to 50 K at pulse amplitude Vamp = 4 V. The pulse conditions are the same as those in Fig. 2. b Nrec as a function of T at pulse base voltage Vbase = −10 V. The inset shows the band diagrams illustrating the hole (blue circles) emission from the potential well at pulse ON stage at T ≳ 30 K.
We finally show the dependence of Irec on the hold time tON of the “pulse ON” stage. For the measurements discussed above, we set tON on the order of millisecond so that all the recombination events are completed within one cycle of the gate pulse. Here, we vary tON in the range of 10 ns to 100 μs to investigate the recombination lifetime. Figure 5a shows Irec and Nrec as a function of tON, measured at 8 K. For this measurement, the Vbase was set at –10 V, corresponding to the initial hole density Nh0 = 6.0 × 1012 cm−2, and Vamp was set at 6 V, corresponding to the density of the introduced electrons Ne = 3.25 × 1012 cm−2. (These Vbase and Vamp conditions are marked by the blue circle in Fig. 3a.)
a Irec (left axis) and density of recombined e-h pairs Nrec (right axis) as a function of the tON for pulse amplitude Vamp = 6 V and base voltage Vbase = −10 V. Circles are the experimental data and the red dashed line is the fitting curve with the recombination time constant τ1 = 30 ns and pre-factor I0(1) = 63.5 nA. b Irec – I(1) as a function of tON. The blue dashed line is the fitting curve with the recombination time constant τ2 = 0.7 μs, the delay time t0 = 0.6 μs, and pre-factor I0(2) = 1.4 nA.
One can see in Fig. 5a that Irec exhibits a two-step rise. The first rise of Irec can be fitted by a simple exponential form of I(1) = I0(1) (1− exp[−tON/τ1]) (red dashed line in the figure) with the time constant τ1 = 30 ns and the pre-factor I0(1) = 63.5 nA, which corresponds to 98% of the maximum value of Irec (= 64.9 nA). To evaluate the second rise part, we plot Irec − I(1) in Fig. 5b. One can see that Irec − I(1) can be fitted by the exponential form with the time constant τ2 = 0.7 μs (blue dashed line).
These results indicate that the present e-h system possesses two different recombination processes. The short (τ1 = 30 ns) and long (τ2 = 0.7 μs) recombination lifetimes respectively are the same order of the high-density unstable e-h plasma58,59 and exciton60 in Si. Noteworthy is that the second process starts to occur only after about 98% of the introduced electrons are recombined, i.e., only after the electron density is reduced down to about 0.7 × 1011 cm−2. The result suggests that the phase of the introduced electrons changes from the plasma (free Fermi gas) to the excitons (bound with a hole) as the recombination proceeds.
The behaviors of the above two (fast and slow) time-constants were also observed by a different measurement technique, the real-time monitoring of the recombination current using a high-speed current amplifier61,62,63. Figure 6a presents the experimental setup. The time constant for the current detection was set at 10 ns, which is the shortest available in our measurement system. The Vamp and Vbase were respectively set at 6 V and –10 V, which are the same conditions as those for Fig. 5. Figure 6b, c, respectively, show the pulse voltage and the resultant recombination current in time-domain irec(t), measured at 8 K. A sharp current spike is observed, which corresponds to the fast recombination process with the time constant of 30 ns in Fig. 5. Figure 6d displays the data of the micro-second range, where the vertical irec(t) axis is magnified. We observe a small current recovery followed by a slow decay, corresponding to the slow process with a time constant of 0.7 μs, agreeing with the data shown in Fig. 5.
a Setup for real-time monitoring. The source/drain electron current is monitored using a high-speed current amplifier. b, c Gate pulse voltage Vg(t) and the resultant recombination current in time domain irec(t) at 8 K. Pulse amplitude Vamp and base voltage Vbase are respectively set at 6 V and –10 V. These pulse-voltage conditions are the same as those for Fig. 5. d Magnified view of the slow-recombination process part.
It should be noted that the phase transition between the plasma and exciton gas in e-h bilayers has been theoretically analyzed using the Monte Carlo simulations64,65,66. The critical density nM for the transition (between the e-h plasma and the dipole exciton gas) is estimated by a simple form of nMae-h ≃ 0.02 (Eq. 3 of ref. 11), where ae-h is the Bohr radius of the dipole exciton. Assuming ae-h = d (≃ 6 nm), where d is the distance between electron and hole layers (Fig. 3d), nM comes to 0.6 × 1011 cm−2. This value is close to the boundary electron density of 0.7 × 1011 cm−2, observed in the measurement.
Although additional measurements, such as temperature dependence and electron- and hole-density dependence (i.e., Vamp and Vbase dependence) are called for to construct the phase diagram, the data reveal that the present e-h system could possess a rich set of configurations, and these can be analyzed by monitoring the recombination current.
In the following, we discuss the features of the present method and the works to be performed in the future.
The drawback of SiO2/Si system is that there is no technology available for the hetero-epitaxy, which prevents us from forming uniform stacked layers of electrons and holes. The alternative solution might be the use of the FD-SOI technology. Using thin SOI films, we can form the electron and hole layers at each (top or bottom) side of the SOI interfaces with SiO235,36,37. However, the SOI film thinned down to nanometer-scale inevitably suffered from non-negligible thickness fluctuation. The state-of-the-art FD-SOI technology provides thin Si films whose thickness fluctuation is about 0.4 nm in standard deviation40. This is already remarkable, but will still be insufficient for the realization of the quantum condensation. In order for the quantum condensation to emerge, charge density fluctuation may have to be reduced to 1 × 1010 cm−2 or even smaller39 and, for this purpose, atomically flat layers are called for. In fact, the standard deviation of the roughness of the graphene sheet formed on the boron nitride film is 0.03 nm41, one order of magnitude smaller than that available in FD-SOI technology.
This is why we proposed the self-organized e-h bilayer formation at the single interface. We emphasize that the thickness fluctuation is due to the spatially uncorrelated interface roughness of the top and bottom interfaces, not the interface roughness itself. If we can make an e-h bilayer in a self-organized way at the single interface, then the electrons and holes are free from the thickness-fluctuation problem, and the spatial configuration of electrons and holes will be determined solely by the electronic correlation and the thermodynamic properties of the e-h system. We expect that our proposed method has the potential to offer such an ideal system.
In the future, we should critically evaluate the effect of the interface roughness itself on the charge density fluctuation. However, as long as we consider the experimental evidence reported in the research field of the strongly interacting electron systems in MOSFETs, the interface roughness does not cause any serious problems for investigating the properties of the system42,43,44.
We next discuss the importance of the bilayer formation in Si. From the viewpoint of the quantum condensation, Si e-h system has both advantage and disadvantage. The advantage is the long recombination time45 owing to the indirect bandgap nature, which gives the e-h system enough time to stabilize down to the ground state, as we have mentioned. (Note that most of the preceding materials used for the condensation experiments, e.g., GaAs and monolayer transition-metal dichalcogenides, have direct bandgap, and thus spatially separated electrons and holes (i.e., e-h bilayer) are indispensable in order to overcome the short recombination lifetime.) The disadvantage, on the other hand, arises from the multi-valley structure of the conduction band, causing the formation of e-h droplets3,6, which is the obstacle against the realization of the BEC of excitons. One way to avoid the droplet formation is the spatial separation of electrons and holes, which increases the strength of repulsive e-e and h-h interactions relative to the attractive e-h interaction, preventing the e-h system from agglomerating into droplets67. (Another way to avoid the droplet formation is the stress application68.) This means that the e-h bilayer formation is important in Si as well, but for a different reason from that of the preceding materials. As we have shown (in Fig. 3), the present method could provide the automatic formation of the bilayer-like e-h configuration at the MOS interface without the annoyance of the Si thickness fluctuation problem in SOIs.
We should emphasize here that the indirect bandgap of Si is critical for the self-organized e-h bilayer created by the present method using the transient response. In the preceding materials, such as graphene and MoS2, the electron and hole layers are separated by the boron nitride insulating spacer, which has a large potential barrier. Therefore, formation of the bilayer and the resultant indirect dipole excitons can be stable by avoiding the recombination (or tunneling) even with the direct bandgap nature. However, in the present method, the barrier separating the electrons and holes is induced by the electric field created in the Si layer, which is not strong enough to suppress the coupling (overlapping of the wave-functions). Therefore, the indirect bandgap and the resultant long recombination time are needed for the present method. In other words, the present transient technique to be performed at the single interface will not be applicable to the direct bandgap materials.
The most important issue to be further studied will be the phase diagram of this e-h coexistence system. For this purpose, the recombination lifetime measurements shown in Fig. 5 have to be extended for a wide range of electron and hole densities, and of the temperature. Based on references11,69, we roughly estimated the characteristic temperature Tc at which the excitons become degenerate. The result was a few Kelvin for the Si (100) interface. This is comparable to those for the GaAs and SiGe hetero e-h bilayers8,20. The recombination lifetime measurements in this temperature range will be particularly important.
With the present simple structure of MOSFETs, the hole current cannot be monitored. Therefore, a modified structure with p-type terminals (like the body contact of the MOSFET) should be prepared. By designing the time chart for the biasing of the drain terminals, the channel currents for both electron and hole layers can be monitored under the e-h bilayer configuration.
In summary, we investigated the electrical formation of the e-h coexisting system at the Si MOSFET interface. Measurements of the recombination current demonstrated that the transient e-h system can be formed at temperatures lower than about 30 K, and the electron and hole densities can be independently controlled by the amplitude and the base of the gate-voltage pulse, respectively. The measurements also indicated that the electrons are located at positions adjacent to the hole layer, at distances on the order of nanometers. In addition, we observed changes in the recombination lifetime as the recombination process proceeds, suggesting that the present e-h system possesses rich set of phases, depending on the electron and hole densities.
In the Vbase range where Irec is nearly linearly varying, e.g., –4 V ≲ Vbase ≲ –1.6 V in Fig. 2, Irec was found to have an additional component originating from the recombination of electrons with holes trapped at the interface defects. Therefore, for the analysis, we have to carefully consider the effects of the interface defects. On the other hand, by using the properties of the interface-defect mediated recombination current, we can estimate the value of Vacc, the threshold voltage of the accumulation-layer formation. Here, we first describe in how to estimate Vacc, and in how the interface-defect mediated recombination currents contribute to Irec and how to compare the slope with the accumulation capacitance model.
Here, we estimate the threshold voltage Vacc for the accumulation-layer formation, and show that the estimated value is consistent with that (Vacc = –1.6 V) obtained in Figs. 2 and 3a.
The Vacc can be expressed as Vacc = VFB – ΔVg, where VFB is the flat-band voltage and ΔVg is the gate voltage, with respect to VFB, required for forming the lowest subband of the hole accumulation layer. In the following, we estimate VFB and ΔVg separately.
The VFB was estimated from the charge pumping (CP) measurements. The CP has been widely used for investigating the interface defects54,61,62,63. In the CP measurements54, a repetitive pulse voltage is applied to the gate so that holes and electrons are alternatively generated at the interface, similarly to the present method. The difference is the rising time tR. In the CP, the tR is set at a sufficiently large value so as to avoid the e-h coexistence. Then, the resultant e-h recombination current, called the CP current ICP, is generated, which flows only via the interface defects (see the potential diagram in Fig. 7a and the figure caption). The ICP is given by ICP = ANitef, where Nit is the density of the interface-defect states that can participate in the CP recombination process. Figure 7b shows the ICP of the present MOSFET taken as a function of Vbase at 8 K. (The Nit converted from ICP is shown on the right axis.) The tR was set at 1 ms. (As a reminder, it was set on the order of 10 ns for Figs. 2–6.) You can see that ICP flows only in a limited Vbase range (–3.4 V < Vbase < –1 V). This is because the lowest value (= Vbase) and the highest value (= Vbase + Vamp) of the gate pulse must be lower and higher than VFB and Vth (threshold voltage of the electron channel), respectively, in order to alternatively generate holes and electrons at the interface (see the inset of Fig. 7b). Therefore, the lower and higher thresholds of the ICP are respectively given by Vth – Vamp and VFB, as indicated by the arrows in Fig. 7b54. From the data, the VFB was estimated to be –1.2 ± 0.1 V. (Note that, from the value of ICP at the plateau, the maximum Nit was estimated to be 3 × 1010 cm–2.)
a Potential diagrams for the charge pumping (CP) sequence in one cycle of the gate pulse. Electrons (red circles) are captured by defect states in the rise step of the pulse (left), and the trapped electrons subsequently recombine with valence-band holes (blue circles) in the fall step (right). Capture of electrons by the interface defects and recombination of the captured electrons with holes are indicated by the dotted arrows. EC and EV are the edges of the conduction and valence bands, respectively. An important point of the CP process is that there is no time period where conduction-band electrons and valence-band holes coexist, which makes the CP process different from the present transient process. b CP current ICP (left axis) and density of interface-defect states Nit (right axis) as a function of pulse base voltage Vbase taken at 8 K with the amplitude Vamp = 4 V, the frequency f = 500 Hz, and the rising time tR = 1 ms. The inset shows the gate pulse for three Vbase regions compared with threshold Vth and flat-band voltages VFB; (i) Vbase < Vth – Vamp, (ii) Vth – Vamp ≤ Vbase ≤ VFB, and (iii) Vbase > VFB. c Band diagrams under the flat-band condition (left) and at the lowest subband formation of the hole accumulation layer (right). In the diagram, ΔVg is the gate voltage, with respect to VFB (flat-band voltage), required for forming the lowest subband of the hole-accumulation layer. The tox, tSi, and Δφs are, respectively, the gate oxide thickness, the accumulation layer thickness, and the surface potential change from the flat-band condition for the lowest-subband formation.
The ΔVg was estimated with the help of the theoretically derived values (from the literature) of the accumulation layer thickness tSi and the surface potential change from the flat-band condition Δφs for the lowest-subband formation (see Fig. 7c). According to the self-consistent calculations of the potential profile and the hole wave-function56,57, these were evaluated to be tSi ≃ 5 nm and Δφs ≃ 20 mV. The ΔVg can then be converted from Δφs as ΔVg = Δφs(Cox + CSi)/Cox, where the Cox = εox/tox and CSi = εSi/tSi with εox, εSi, and tox being the dielectric constants of the gate oxide and Si, and the gate-oxide thickness, respectively. Using εox = 3.9ε0, εSi = 11.9ε0 (ε0 is the dielectric constant in vacuum) and tox = 30 nm, the ΔVg was estimated to be 0.4 V.
In conclusion, we obtained Vacc = VFB – ΔVg = –1.6 ± 0.1 V, consistent with the value obtained in Figs. 2 and 3a.
Here, we show that there is an additional component in Irec, and it originates from the CP recombination. We also show how to evaluate the slope of Nrec vs Vbase curve in order to compare it with the accumulation capacitance model.
In Fig. 8, we show with the black line the Irec – Vbase characteristics shown in Fig. 2 in the Vbase range from –4 V to –0.5 V. For comparison, ICP shown in Fig. 7b is replotted with the red line. Nrec and Nit converted from Irec and ICP are also shown on the right axis. These two (black and red) characteristics were taken with the same gate pulse conditions except for the rising time tR, which was 40 ns and 1 ms for the black and red lines, respectively.
The density of recombined e-h pairs Nrec and density of interface-defect states Nit are respectively converted from Irec and ICP, and shown on the right axis. The rising time tR was set at 40 ns and 1 ms, respectively, for the black and red curves. Pulse amplitude Vamp and f are 4 V and 500 Hz, respectively. In the Vbase range of –3.4 V < Vbase < –1 V, the Nrec has an additional component originating from the CP recombination (hatched part). In the Vbase range of –4 V < Vbase < –3.4 V, the Nrec is not influenced by the CP recombination. The slope in this Vbase region was found to agree with –Cg,h/e, where Cg,h is the accumulation-layer capacitance. In addition, the offset value of Vbase obtained by extrapolating the slope (blue dashed line) was found to agree with the Vacc estimated in Methods section “Threshold voltage for accumulation-layer formation”. Vth and VFB are, respectively, the threshold and flat-band voltages.
One can see that Nrec (black line) has two features, a kink and tail, respectively, at Vbase = –3.4 V and –1.2 V, as indicated by the vertical arrows. One can also see that the values of Vbase at which the kink and the tail appear are coincident with the thresholds for Nit (red line). This indicates that the Nrec curve has an additional component originating from the recombination via the interface defects. This means that Nrec can be decomposed into two components. One is due to the e-h recombination dominated by the holes in the accumulation layer, which follows Nrec = – Cg,h (Vbase – Vacc)/e (indicated by the blue dashed line in Fig. 8). The other is due to the CP process where electrons are recombined with holes trapped at the interface defects (indicated by the hatching).
From the above analysis, one understands that only the limited range of Vbase, –4 V < Vbase < –3.4 V (= Vth – Vamp), gives us Nrec which is not influenced by the interface-defect mediated current (CP current). What we have found is that the slope in this Vbase region agrees with –Cg,h/e, where Cg,h is the hole accumulation-layer capacitance, and the resultant offset value of the Vbase, obtained by extrapolating the slope (blue dashed line), agrees with the hole accumulation-layer threshold Vacc (as explained in Methods section “Threshold voltage for accumulation-layer formation”). This means that the major Irec component, i.e., that not related to the CP process, is well described by the accumulation capacitance model.
The n-channel MOSFETs were fabricated on a Si(100) substrate. The channel length, width and gate oxide thickness were, respectively, 50 μm, 500 μm and 30 nm, and the substrate doping (boron) concentration was of the order of 1015 cm−3. The gate oxide was formed in a dry oxygen ambient at 950 °C for 50 min. The gate was made of phosphorus-doped poly-Si and the fabrication was finalized with the forming gas (N2:H2 = 2:1) treatment at 450 °C for 30 min. The interface defect density was estimated to be 3 × 1010 cm−2 from the CP measurements described above.
The gate pulse was generated with the arbitrary function generator Tektronix AFG31102. The recombination current was measured in a low-temperature probing station with the source monitor units (SMUs) of the semiconductor parameter analyzer Keysight B1500A. Basically, the SMUs measure the charge Q originating from the current I to be measured with the long time period TP, and outputs the current I = Q/TP. Owing to this simple operation principle, it enables us to measure the (time-averaged) recombination current with a very high precision (at the cost of losing the information of the time domain).
For the real-time monitoring of irec(t), a high-speed current amplifier FEMTO DHPCA-100 was used. The time constant for the current detection was set at 10 ns, which is the shortest in the present measurement system.
The lattice temperature T of the device was measured and calibrated by using a commercially available Si diode thermometer.
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Keldysh, L. V. & Kozlov, A. N. Collective properties of excitons in semiconductors. Sov. Phys. JETP 27, 521–528 (1968).
ADS Google Scholar
Jeffries, C. D. Electron-hole condensation in semiconductors. Science 189, 955–964 (1975).
Article ADS Google Scholar
Rice, T. M. The electron-hole liquid in semiconductors: theoretical aspects. Solid State Phys. 32, 1–86 (1978).
Article Google Scholar
Hensel, J. C., Phillips, T. G. & Thomas, G. A. The electron-hole liquid in semiconductors: experimental aspects. Solid State Phys. 32, 87–314 (1978).
Article Google Scholar
Keldysh, L. V. The electron-hole liquid in semiconductors. Contemp. Phys. 27, 395–428 (1986).
Article ADS Google Scholar
Sibeldin, N. N. Electron-hole liquid in semiconductors and low-dimensional structures. Phys. Uspekhi 60, 1147–1179 (2017).
Article ADS Google Scholar
Fukuzawa, T., Mendez, E. E. & Hong, J. M. Phase transition of an exciton system in GaAs coupled quantum wells. Phys. Rev. Lett. 64, 3066–3069 (1990).
Article ADS Google Scholar
Butov, L. V., Lai, C. W., Ivanov, A. L., Gossard, A. C. & Chemla, D. S. Towards Bose-Einstein condensation of excitons in potential traps. Nature 417, 47–52 (2002).
Article ADS Google Scholar
Snoke, D., Denev, S., Liu, Y., Pfeiffer, L. & West, K. Long-range transport in excitonic dark states in coupled quantum wells. Nature 418, 754–757 (2002).
Article ADS Google Scholar
Du, L. et al. Evidence for a topological excitonic insulator in InAs/GaSb bilayers. Nat. Commun. 8, 1971 (2017).
Article ADS Google Scholar
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 5, 4555 (2014).
Article ADS Google Scholar
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Article ADS MathSciNet Google Scholar
Jiang, Y., Chen, S., Zheng, W., Zheng, B. & Pan, A. Interlayer exciton formation, relaxation, and transport in TMD van der Waals heterostructures. Light Sci. Appl. 10, 72 (2021).
Article ADS Google Scholar
Wang, Z. et al. Evidence of high-temperature exciton condensation in two-dimensional atomic double layers. Nature 574, 76–80 (2019).
Article ADS Google Scholar
Ma, L. et al. Strongly correlated excitonic insulator in atomic double layers. Nature 598, 585–589 (2021).
Article ADS Google Scholar
Liu, X., Watanabe, K., Taniguchi, T., Halperin, B. I. & Kim, P. Quantum Hall drag of exciton condensate in graphene. Nat. Phys. 13, 746–750 (2017).
Article Google Scholar
Burg, G. W. et al. Strongly enhanced tunneling at total charge neutrality in double-bilayer graphene-WSe2 heterostructures. Phys. Rev. Lett. 120, 177702 (2018).
Article ADS Google Scholar
Liu, X. et al. Crossover between strongly coupled and weakly coupled exciton superfluids. Science 375, 205–209 (2022).
Article ADS Google Scholar
Banerjee, S. K., Register, L. F., Tutuc, E., Reddy, D. & MacDonald, A. H. Bilayer pseudospin field-effect transistor (BiSFET): a proposed new logic device. IEEE Electron Device Lett. 30, 158–160 (2009).
Article ADS Google Scholar
Conti, S. et al. Electron-hole superfluidity in strained Si/Ge type II heterojunctions. NPJ Quant. Mat. 6, 41 (2021).
Article ADS Google Scholar
Sun, Z., Kaneko, T., Golež, D. & Millis, A. J. Second-order Josephson effect in excitonic insulators. Phys. Rev. Lett. 127, 127702 (2021).
Article ADS Google Scholar
Anantharaman, S. B., Jo, K. & Jariwala, D. Exciton-photonics: from fundamental science to applications. ACS Nano 15, 12628–12654 (2021).
Article Google Scholar
Reddy, D., Register, L. F., Tutuc, E. & Banerjee, S. K. Bilayer pseudospin field-effect transistor: applications to Boolean logic. IEEE Trans. Electron Devices 57, 755–764 (2010).
Article ADS Google Scholar
Nandi, D., Finck, A. D. K., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Exciton condensation and perfect Coulomb drag. Nature 488, 481–484 (2012).
Article ADS Google Scholar
Patra, B. et al. Cryo-CMOS circuits and systems for quantum computing applications. IEEE J. Sol. State Circuits 53, 309–321 (2018).
Article ADS Google Scholar
Beckers, A., Jazaeri, F. & Enz, C. Characterization and modeling of 28-nm bulk CMOS technology down to 4.2 K. IEEE J. Electron Devices Soc. 6, 1007–1018 (2018).
Article Google Scholar
Xue, X. et al. CMOS-based cryogenic control of silicon quantum circuits. Nature 593, 205–210 (2021).
Article ADS Google Scholar
Shah, J., Combescot, M. & Dayem, A. H. Investigation of exciton-plasma Mott transition in Si. Phys. Rev. Lett. 38, 1497–1500 (1977).
Article ADS Google Scholar
Forchel, A., Laurich, B., Wagner, J., Schmid, W. & Reinecke, T. L. Systematics of electron-hole liquid condensation from studies of silicon with varying uniaxial stress. Phys. Rev. B 25, 2730–2747 (1982).
Article ADS Google Scholar
Norris, G. B. & Bajaj, K. K. Exciton-plasma Mott transition in Si. Phys. Rev. B 26, 6706–6710 (1982).
Article ADS Google Scholar
Smith, L. M. & Wolf, J. P. Time-resolved study of electron-hole plasmas near the liquid-gas critical point in Si: evidence for a second condensed phase. Phys. Rev. B 51, 7521–7543 (1995).
Article ADS Google Scholar
Tajima, M. & Ibuka, S. Luminescence due to electron-hole condensation in silicon-on-insulator. J. Appl. Phys. 84, 2224–2228 (1998).
Article ADS Google Scholar
Nihonyanagi, S. & Kanemitsu, Y. Enhanced luminescence from electron-hole droplets in silicon nanolayers. Appl. Phys. Lett. 85, 5721–5723 (2004).
Article ADS Google Scholar
Pauc, N., Calvo, V., Eymery, J., Fournel, F. & Magnea, N. Two-dimensional electron-hole liquid in single Si quantum wells with large electronic and dielectric confinement. Phys. Rev. Lett. 92, 236802 (2004).
Article ADS Google Scholar
Takashina, K., Gaillard, B., Ono, Y. & Hirayama, Y. Low-temperature characteristics of ambipolar SiO2/Si/SiO2 hall-bar devices. Jpn. J. Appl. Phys. 46, 2596–2598 (2007).
Article ADS Google Scholar
Prunnila, M., Laakso, S. J., Kivioja, J. M. & Ahopelto, J. Electrons and holes in Si quantum well: a room-temperature transport and drag resistance study. Appl. Phys. Lett. 93, 112113 (2008).
Article ADS Google Scholar
Takashina, K. et al. Electrons and holes in a 40 nm thick silicon slab at cryogenic temperatures. Appl. Phys. Lett. 94, 142104 (2009).
Article ADS Google Scholar
Narozhny, B. N. & Levchenko, A. Coulomb drag. Rev. Mod. Phys. 88, 025003 (2016).
Article ADS Google Scholar
Ho, D. Y. H., Yudhistira, I., Hu, B. Y. & Adam, S. Theory of Coulomb drag in spatially inhomogeneous 2D materials. Commun. Phys. 1, 41 (2018).
Article Google Scholar
Schwarzenbach, W., Nguyen, B. Y., Allibert, F., Girard, C. & Maleville, C. Ultra-thin body & buried oxide SOI substrate development and qualification for fully depleted SOI device with back bias capability. Solid State Electron. 117, 2–9 (2016).
Article ADS Google Scholar
Xie, J. et al. Scanning tunnelling microscopy and spectroscopy of ultra-flat graphene on hexagonal boron nitride. Nat. Mater. 13, 282–285 (2011).
Article ADS Google Scholar
Kravchenko, S. V., Kravchenko, G. V., Furneaux, J. E., Pudalov, V. M. & D’Iorio, M. Possible metal-insulator transition at B = 0 in two dimensions. Phys. Rev. B 50, 8039–8042 (1994).
Article ADS Google Scholar
Abrahams, E., Kravchenko, S. V. & Sarachik, M. P. Colloquium: metallic behavior and related phenomena in two dimensions. Rev. Mod. Phys. 73, 251–266 (2001).
Article ADS Google Scholar
Shashkin, A. A. & Kravchenko, S. V. Recent developments in the field of the metal-insulator transition in two dimensions. Appl. Sci. 9, 1169 (2019).
Article Google Scholar
Hammond, R. B. & Silver, R. N. Temperature dependence of the exciton lifetime in high-purity silicon. Appl. Phys. Lett. 36, 68–71 (1980).
Article ADS Google Scholar
Camescasse, F. X. et al. Ultrafast electron redistribution through Coulomb scattering in undoped GaAs: experiment and theory. Phys. Rev. Lett. 77, 5429–5432 (1996).
Article ADS Google Scholar
Suzuki, T. & Shimano, R. Cooling dynamics of photoexcited carriers in Si studied using optical pump and terahertz probe spectroscopy. Phys. Rev. B 83, 085207 (2011).
Article ADS Google Scholar
Suzuki, T. & Shimano, R. Time-resolved formation of excitons and electron-hole droplets in Si studied using terahertz spectroscopy. Phys. Rev. Lett. 103, 057401 (2009).
Article ADS Google Scholar
Saks, N. S. & Nordbryhn, A. Time dependence of depletion region formation in phosphorus-doped silicon MOS devices at cryogenic temperatures. J. Appl. Phys. 50, 6962–6968 (1979).
Article ADS Google Scholar
Tewksbury, S. K. Transient response of n-channel metal-oxide-semiconductor field-effect transistors during turnon at 10–25 °K. J. Appl. Phys. 53, 3865–3872 (1982).
Article ADS Google Scholar
Tewksbury, S. K. Formation of high density electron-hole plasma in silicon metal-oxide-semiconductor transistors below 25 °K. J. Appl. Phys. 54, 868–875 (1983).
Article ADS Google Scholar
Ouisse, T. et al. Adaptation of the charge pumping technique to gated p-i-n diodes fabricated on silicon on insulator. IEEE Trans. Electron Devices 38, 1432–1444 (1991).
Article ADS Google Scholar
Van den bosch, G., Groeseneken, G. & Maes, H. E. On the geometric component of charge-pumping current in MOSFET’s. IEEE Electron Device Lett. 14, 107–109 (1993).
Article ADS Google Scholar
Groeseneken, G., Maes, H. E., Beltran, N. & DeKeersmaecker, R. F. A reliable approach to charge-pumping measurements in MOS transistors. IEEE Trans. Electron Devices 31, 42–53 (1984).
Article ADS Google Scholar
O’Donnell, K. P. & Chen, X. Temperature dependence of semiconductor band gaps. Appl. Phys. Lett. 58, 2924–2926 (1991).
Article ADS Google Scholar
Ando, T. Density-functional calculation of sub-band structure in accumulation and inversion layers. Phys. Rev. B 13, 3468–3477 (1976).
Article ADS Google Scholar
Ando, T., Fowler, A. B. & Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 54, 437–672 (1982).
Article ADS Google Scholar
Steranka, F. M. & Wolfe, J. P. Spatial expansion of electron-hole plasma in Si. Phys. Rev. B 34, 1014–1030 (1986).
Article ADS Google Scholar
Pauc, N., Calvo, V., Eymery, J., Fournel, F. & Magnea, N. Electronic and optical properties of Si/SiO2 nanostructures. I. Electron-hole collective processes in single Si/SiO2 quantum wells. Phys. Rev. B 72, 205324 (2005).
Article ADS Google Scholar
Yoo, J. Y. & Shimano, R. Lifetime measurement of excitons in Si by terahertz time-domain spectroscopy with high spectral resolution. J. Inf. Milli. THz Waves 35, 110–117 (2014).
Article Google Scholar
Hori, M., Watanabe, T., Tsuchiya, T. & Ono, Y. Analysis of electron capture process in charge pumping sequence using time domain measurements. Appl. Phys. Lett. 105, 261602 (2014).
Article ADS Google Scholar
Hori, M., Watanabe, T., Tsuchiya, T. & Ono, Y. Direct observation of electron emission and recombination processes by time domain measurements of charge pumping current. Appl. Phys. Lett. 106, 041603 (2015).
Article ADS Google Scholar
Watanabe, T., Hori, M., Tsuchiya, T., Fujiwara, A. & Ono, Y. Time-domain charge pumping on silicon-on-insulator MOS devices. Jpn. J. Appl. Phys. 56, 011303 (2017).
Article ADS Google Scholar
De Palo, S., Rapisarda, F. & Senatore, G. Excitonic condensation in a symmetric electron-hole bilayer. Phys. Rev. Lett. 88, 206401 (2002).
Article ADS Google Scholar
Schleede, J., Filinov, A., Bonitz, M. & Fehske, H. Phase diagram of bilayer electron-hole plasmas. Contrib. Plasma Phys. 52, 819–826 (2012).
Article ADS Google Scholar
Maezono, R., Ríos, P. L., Ogawa, T. & Needs, R. J. Excitons and biexcitons in symmetric electron-hole bilayers. Phys. Rev. Lett. 110, 216407 (2002).
Article ADS Google Scholar
Eisenstein, J. P. & MacDonald, A. H. Bose-Einstein condensation of excitons in bilayer electron systems. Nature 432, 691–694 (2004).
Article ADS Google Scholar
Naka, N., Omachi, J. & Kuwata-Gonokami, M. Suppressed formation of electron-hole droplets in diamond under a strain field. Phys. Rev. B 76, 193202 (2007).
Article ADS Google Scholar
Snoke, D. & Kavoulakis, G. M. Bose-Einstein condensation of excitons in Cu2O: progress over 30 years. Rep. Prog. Phys. 77, 116501 (2014).
Article ADS Google Scholar
Download references
The authors thank M. Tabe, T. Tsuchiya, and D. Moraru for their valuable comments. This work was partially supported by JSPS KAKENHI (JP16H06087, JP20H02203, JP20H00241, and JP22K18294).
Research Institute of Electronics, Shizuoka University, Johoku, Naka-ku, Hamamatsu, 432-8011, Japan
Masahiro Hori, Manjakavahoaka Razanoelina & Yukinori Ono
Graduate School of Science and Technology, Shizuoka University, Johoku, Naka-ku, Hamamatsu, 432-8011, Japan
Masahiro Hori, Jinya Kume & Yukinori Ono
Graduate School of Natural Science and Technology, Shimane University, Nishi-Kawatsucho, Matsue, 690-8504, Japan
Hiroyuki Kageshima
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
M.H. and J.K. measured the device; M.H. analyzed the data; M.H. and Y.O. wrote the manuscript; M.H., M.R. H.K., and Y.O. discussed the results; M.H. supervised the project.
Correspondence to Masahiro Hori.
The authors declare no competing interests.
Communications Physics thanks Kantimay Das Gupta and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and permissions
Hori, M., Kume, J., Razanoelina, M. et al. Electrical control of transient formation of electron-hole coexisting system at silicon metal-oxide-semiconductor interfaces. Commun Phys 6, 316 (2023). https://doi.org/10.1038/s42005-023-01428-1
Download citation
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01428-1
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Advertisement
© 2024 Springer Nature Limited
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.